| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 파이썬
- 알고리즘 풀이
- c++
- 알고리즘 문제
- HTML
- java
- AWS
- es6
- django rest framework
- API
- web
- 백준
- DRF
- Git
- PYTHON
- Algorithm
- 알고리즘 연습
- react
- MAC
- form
- 장고
- 파이썬 알고리즘
- Baekjoon
- django widget
- django ORM
- 알고리즘
- javascript
- CSS
- js
- Django
- Today
- Total
수학과의 좌충우돌 프로그래밍
[Algorithm] Kruskal 알고리즘 본문
Kruskal 알고리즘이란?
Kruskal 알고리즘이란, 그래프에서 MST 를 찾는 알고리즘입니다. MST 가 무엇인지 모르신다면 아래 링크를 참고해주세요.
[Algorithm] Spanning Tree 와 MST, 스패닝 트리와 최소 스패닝 트리
Spanning Tree 란? Spanning Tree 란 스패닝 트리라고 읽으며 다른 말로 신장트리 라고도 합니다. 이는 그래프 내의 모든 정점을 포함하는 트리를 말합니다. 그래프의 일부 간선을 이용해 만든 트리로서 항상 그래..
ssungkang.tistory.com
이 알고리즘은 MST 를 찾기 위해서 greedy 하게 접근합니다. greedy 하게 접근한다는 말은 현재 순간에 최적의 선택을 한다는 의미인데 최소 비용으로 각 노드를 연결하기 위해서는 어떤 선택이 최적의 선택일까요? 바로 비용이 가장 적은 간선을 택하는 것입니다.
greedy 하게 접근하기 위해서는 항상 이러한 접근이 해답을 구할 수 있는지를 검증해야 합니다. 자세하게 다루지는 않지만 이미 검증이 되었습니다.
알고리즘 과정
- 우선 비용이 낮은 간선부터 선택해야 하니 그래프를 가중치의 오름차순으로 정렬합니다.
- 정렬된 간선 리스트에서 앞에서 부터 순서대로 사이클을 형성하지 않는 간선을 선택합니다.
아래와 같은 상황에서
Kruskal 알고리즘이 MST 를 어떻게 찾는지 따라가보도록 하겠습니다.
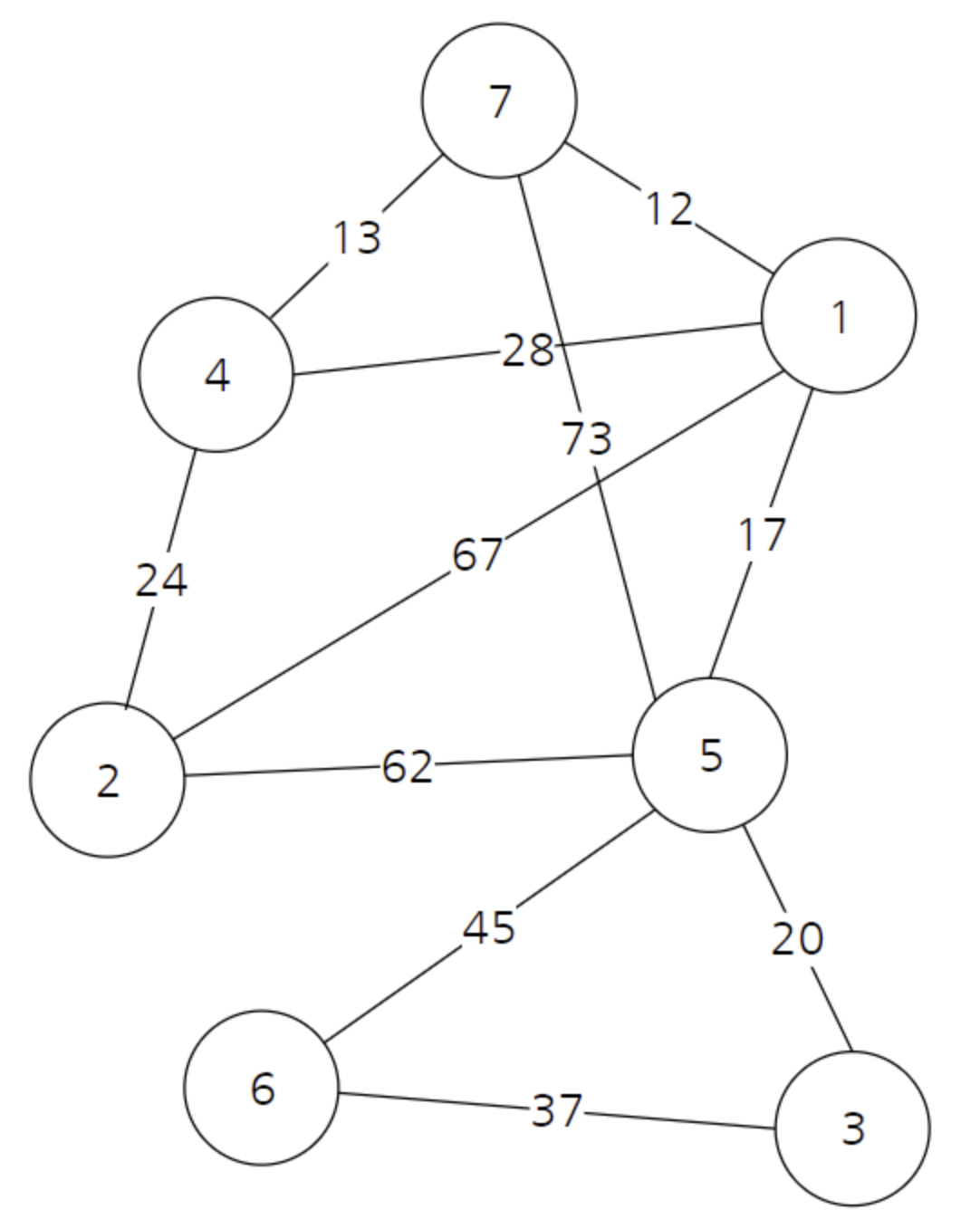
모든 간선에 대해서 검사를 시행해야합니다.
우선 가중치를 오름차순으로 정렬한 후, 각 간선에 대해서 포함여부를 결정해줍니다. 물론 포함여부를 결정하는 요인은 사이클 생성 유무에 따라 결정됩니다.
| 첫번째 노드 | 두번째 노드 | 가중치 | 포함 여부 |
|---|---|---|---|
| 1 | 7 | 12 | O |
| 4 | 7 | 13 | O |
| 1 | 5 | 17 | O |
| 3 | 5 | 20 | O |
| 2 | 4 | 24 | O |
| 1 | 4 | 28 | X |
| 3 | 6 | 37 | O |
| 5 | 6 | 45 | X |
| 2 | 5 | 62 | X |
| 1 | 2 | 67 | X |
| 5 | 7 | 73 | X |
따라서 포함한 간선의 가중치를 모두 더하면,
12+13+17+20+24+28+37+45+62+67+73 = 123 이 됩니다.
구현
Edge 라는 간선 클래스를 만들어줍니다. 해당 클래스는 양쪽 노드와 가중치를 저장하고 있으며 비교 연산자를 오버라이딩 함으로서 가중치에 대한 오름차순으로 정렬을 합니다.
사이클 유무를 판별하기 위해서는 Union-Find알고리즘을 사용하였습니다.
[Algorithm] 유니온 파인드(Union - Find)
유니온 파인드 알고리즘이란? 그래프 알고리즘의 일종으로서 상호 배타적 집합, Disjoint-set 이라고도 합니다. 여러 노드가 존재할 때 어떤 두 개의 노드를 같은 집합으로 묶어주고, 다시 어떤 두 노드가 같은 집..
ssungkang.tistory.com
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
int parent[1000000];
int Find(int x){
if (x==parent[x]) return x;
else {
int y = Find(parent[x]);
parent[x] = y;
return y;
}
}
void Union (int x, int y){
y = Find(y);
x = Find(x);
if (x!=y){
parent[y] = x;
}
}
class Edge {
public:
int node[2];
int distance;
Edge(int a,int b,int distance){
this->node[0] = a;
this->node[1] = b;
this->distance = distance;
}
//연산자 오버로딩
bool operator<(const Edge &edge) const {
return (this->distance) < (edge.distance);
}
};
int main(){
// 노드 수와 엣지 수
int n=7;
int m =11;
vector <Edge> v;
v.push_back(Edge(1,7,12));
v.push_back(Edge(1,4,28));
v.push_back(Edge(1,2,67));
v.push_back(Edge(1,5,17));
v.push_back(Edge(2,4,24));
v.push_back(Edge(2,5,62));
v.push_back(Edge(3,5,20));
v.push_back(Edge(3,6,37));
v.push_back(Edge(4,7,13));
v.push_back(Edge(5,6,45));
v.push_back(Edge(5,7,73));
// 위의 연산자 오버로딩
sort(v.begin(), v.end());
for (int i=1;i<=n;i++){
parent[i] = i;
}
int sum = 0;
for (int i=0;i<v.size();i++){
// 두 노드의 부모가 다르면, 즉 같은 집합안에 있지 않으면 사이클이 생기지 않는다.
if (Find(v[i].node[0]) != Find(v[i].node[1])){
sum += v[i].distance;
Union(v[i].node[0], v[i].node[1]);
}
}
cout << sum << "\n";
// 123
}
'알고리즘 > 이론' 카테고리의 다른 글
| [Algorithm] 벨만포드(Bellman-Ford) 알고리즘 (0) | 2019.11.07 |
|---|---|
| [Algorithm] Prim 알고리즘 (1) | 2019.11.05 |
| [Algorithm] Spanning Tree 와 MST, 스패닝 트리와 최소 스패닝 트리 (0) | 2019.10.04 |
| [Algorithm] 세그먼트 트리(Segment Tree) (3) | 2019.09.27 |
| [Algorithm] 비트마스크 (0) | 2019.09.23 |




