| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- web
- 알고리즘 풀이
- django widget
- DRF
- CSS
- java
- Django
- es6
- c++
- PYTHON
- MAC
- HTML
- form
- 파이썬 알고리즘
- 알고리즘 연습
- 백준
- Algorithm
- AWS
- 장고
- react
- 알고리즘
- javascript
- API
- 파이썬
- django ORM
- 알고리즘 문제
- js
- Git
- Baekjoon
- django rest framework
- Today
- Total
수학과의 좌충우돌 프로그래밍
[Algorithm] 플로이드 와샬(Floyd-Warshall) 알고리즘 본문
그래프에서 정점끼리의 최단 경로를 구하는 방법은 여러가지가 있습니다. 플로이드 와샬 알고리즘에 대해서 알아보기 전에 이에 대해서 간단히 살펴보도록 하겠습니다.
-
하나의 정점에서 다른 하나의 정점까지의 최단 경로를 구하는 문제
single source and single destination shortest path problem
-
하나의 정점에서 다른 모든 정점까지의 최단 경로를 구하는 문제
single source shortest path problem
-
하나의 목적지로가는 모든 최단 경로를 구하는 문제
single destination shortest path problem
-
모든 최단 경로를 구하는 문제
all pairs shortest path problem
Floyd-Warshall 알고리즘이란?
Floyd-Warshall 알고리즘이란, 위 경우에서 마지막에 해당하는 모든 최단 경로를 구하는 방법 입니다. 다익스트라와 벨만포드가 두 번째에 해당하는 하나의 정점에서 다른 모든 정점까지의 최단 경로를 구하는 방법 과는 다릅니다.
알고리즘
Floyd-Warshall 알고리즘을 통해 모든 최단 경로를 구할 수 있습니다. 그러기 위해서 이 정보를 저장할 인접행렬 W 를 만들어주도록 합시다. 인접행렬 W의 크기는 노드의 개수 V에 대해 V X V 의 크기를 가지며, W[i][j] 는 i 번째 노드부터 j 번째 노드까지 가중치 가 됩니다.
다음 그래프에 대해서는 인접행렬 W가 아래와 같이 생기게 됩니다.

0 3 8 INF -4
INF 0 INF 1 7
INF 4 0 INF INF
2 INF -5 0 INF
INF INF INF 6 0
이 때 INF 는 무한대로 이동하는 경로가 없다는 의미입니다.
이를 통해 최단경로 행렬 D 를 만들 수 있습니다.
0 1 -3 2 -4
3 0 -4 1 -1
7 4 0 5 3
2-1 -5 0 -2
해당 행렬 D[i][j] 는 i 번째 노드에서 j 번째 노드까지의 최단 경로 를 의미합니다. 예를 들어 1 에서 3 까지의 최단경로를 보면 -3 이고 이는 1->5->4->3 으로 이동할 경우, -4+6+-5 = -3 이 됨을 알 수 있습니다.
그렇다면 W 인접행렬을 통해 D 최단경로 행렬을 어떻게 만들 수 있을까요?
정점 집합 {1,...,n} 에 대해서 i,j 가 V 에 포함될 때 i와 j사이에 정점 집합 V 에 속하는 모든 정점을 넣어보고 경로의 값이 가장 작아지는 경로를 찾는다.
다음과 같이 언어로 보는 것보단 수식으로 보는게 더 이해하기 쉽습니다.

이 때 dij^(k) 를 k 라는 정점을 이번에 추가하였을 때 i 정점부터 j 정점까지의 최단경로 라고 정의합니다.
즉 k 라는 정점을 새로 추가하였을 때 i 정점부터 j 정점까지의 최단경로는 기존의 i 정점 부터 j 정점까지 이동했던 경로 와 i 정점부터 k 정점까지의 최단 경로 + k 정점부터 j 정점까징의 최단 경로 중 최소값이 됩니다.
다음과 같은 방법으로 플로이드 와샬 알고리즘은 중간 정점을 모두 실험해보게 됩니다.
전체적인 수도코드는 다음과 같습니다.
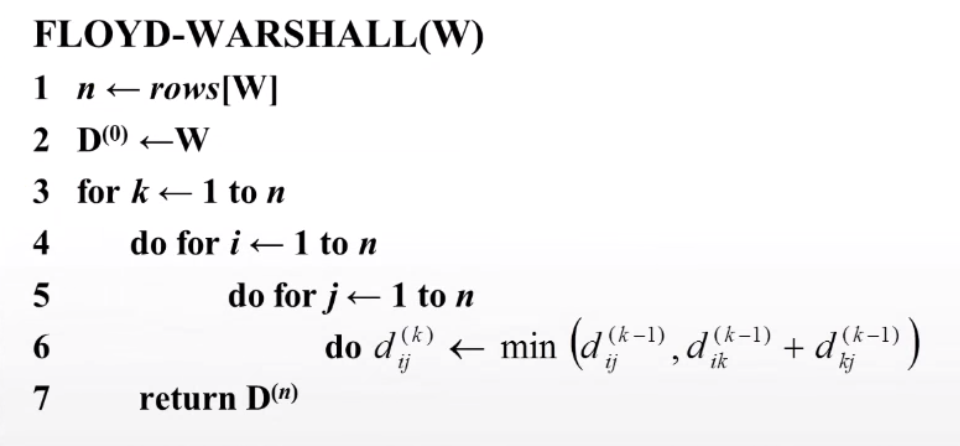
D 행렬의 변화를 전부 다 확인하기는 힘들 것 같고 W 에 해당하는 D(0) 가 D(1) 으로 바뀌는 과정만 같이 보도록 하겠습니다.
// D(0)
0 3 8 INF -4
INF 0 INF 1 7
INF 4 0 INF INF
2 INF -5 0 INF
INF INF INF 6 0
// D(1)
0 3 8 INF -4
INF 0 INF 1 7
INF 4 0 INF INF
2 5 -5 0 -2
INF INF INF 6 0
바뀐 부분을 살펴보면 D[3][1] , D[3][4] 입니다. 4번 정점는 1번 정점를 통해서 2번 정점와 5번 정점으로 갈 수 있게 되었기 때문에 값이 갱신되었고 각 값은 5,-2 입니다.
Floyd-Warshall 경로구하기
최단 경로 행렬 D 를 통해 i 번째 정점에서 j 번째 정점까지 최단경로를 구할 수 있었습니다. 정확히는 최단경로로 갈 때의 가중치를 구하는 것이기 때문에 어떤 정점을 거쳐 가는지는 알 수 없습니다.
따라서 이를 위해 직전 정점 행렬 pi 를 정의해보도록 합시다.
pi[i][j] 는 i 정점에서 j 정점까지의 경로에서 j 정점 직전에 나오는 정점을 의미합니다.
예를 들어 1에서 3까지의 경로를 구해보도록 하겠습니다. 예시를 위해 완성된 pi 행렬을 살펴보면 아래와 같습니다.
- 3 4 5 1
4 - 4 2 1
4 3 - 2 1
4 3 4 - 1
4 3 4 5 -
우선 1 정점에서 출발해서 3 정점에서 끝나므로 경로의 시작은 1, 끝은 3 입니다. 3 직전에 오는 정점은 pi[0][2] 인 4가 됩니다. ( index를 0부터 시작하기 때문에 하나씩 차이가 납니다. )
현재 경로는 1 -> 4 -> 3 이 됩니다.
이제 다시 1 정점에서 4 정점 까지의 경로를 구하기 위해 pi[0][3] 의 값 5를 참조합니다.
현재 경로는 1-> 5 -> 4 -> 3 이 됩니다.
1 정점에서 5정점까지의 경로를 구하기 위해 pi[0][4] 의 값 1 을 참조합니다.
경로가 1-> 1 로 같은 정점이 연속적으로 나온다는 의미는 경로가 완성되었음을 의미합니다.
따라서 완성된 경로는 1-> 5 -> 4 -> 3 가 됩니다.
직전 정점 행렬 pi 가 주어졌을 때 경로를 구하는 방법을 알았으니 pi 행렬을 만들어보도록 합시다.
pi 행렬도 D 행렬과 마찬가지로 가장 바깥 for 문이 돌면서 갱신이 됩니다.
먼저 pi(0) 부터 본다면 다음과 같습니다.
- 1 1 - 1
- - - 2 2
- 3 - - -
4 - 4 - -
- - - 5 -
W[i][j] 의 값이 존재한다면, 즉 i 정점에서 j 정점까지의 경로가 있다면 출발정점 i 를 넣어줍니다.
다음으로 pi(1) 은 다음과 같습니다.
- 1 1 - 1
- - - 2 2
- 3 - - -
4 1 4 - 1
- - - 5 -
1번 정점을 통해 i 에서 j 까지 경로가 생겼다면 pi[i][j] 에 1 을 넣어주도록 합시다.
마찬가지로 pi(k) 에 대해서 k 번 정점을 통해서 i 에서 j 까지 경로가 생겼고 그 경로가 최단경로라면 pi[i][j] 에 k 를 넣어주도록 합니다.
이 과정을 반복한다면 다음과 같습니다.
// pi(2)
- 1 1 2 1
- - - 2 2
- 3 - 2 2
4 1 4 - 1
- - - 5 -
// pi(3)
- 1 1 2 1
- - - 2 2
- 3 - 2 2
4 3 4 - 1
- - - 5 -
// pi(4)
- 1 4 2 1
4 - 4 2 1
- 3 - 2 1
4 3 4 - 1
- - - 5 -
구현
위에서 정의했던 행렬 D 를 graph 행렬로 정의하고, 행렬 pi 를 before 행렬로 정의하였습니다.
#include <iostream>
using namespace std;
#define INF 987654321
#define NIL -1
#define MAX 101
int graph[MAX][MAX];
int before[MAX][MAX];
void floyd(int n){
for (int mid=1;mid<=n;mid++){
for (int start=1;start<=n;start++){
for (int end=1;end<=n;end++){
if (graph[start][end] > graph[start][mid] + graph[mid][end]){
// 더 가까운 경로가 있을 경우 최신화
graph[start][end] = graph[start][mid] + graph[mid][end];
// 직전정점 행렬 최신화
before[start][end] = before[mid][end];
}
}
}
}
}
int main(){
// n: 정점의 수, m: 간선의 수
int n,m;
cin >> n >> m;
// graph 와 before 초기화
for (int i=1;i<=n;i++){
for (int j=1;j<=n;j++){
graph[i][j] = MAX;
if (i==j) graph[i][j] = 0;
before[i][j] = NIL;
}
}
for (int i=0;i<m;i++){
int node1, node2, w;
cin >> node1 >> node2 >> w;
graph[node1][node2] = w;
before[node1][node2] = node1;
}
cout << "초기값\n";
for (int i=1;i<=n;i++){
for (int j=1;j<=n;j++){
cout << graph[i][j] << "\t";
}
cout << "\n";
}
cout << "\n";
for (int i=1;i<=n;i++){
for (int j=1;j<=n;j++){
cout << before[i][j] << "\t";
}
cout << "\n";
}
floyd(n);
cout << "최종값\n";
for (int i=1;i<=n;i++){
for (int j=1;j<=n;j++){
cout << graph[i][j] << "\t";
}
cout << "\n";
}
cout << "\n";
for (int i=1;i<=n;i++){
for (int j=1;j<=n;j++){
cout << before[i][j] << "\t";
}
cout << "\n";
}
}
초기값
0 3 8 101 -4
101 0 101 1 7
101 4 0 101 101
2 101 -5 0 101
101 101 101 6 0
-1 1 1 -1 1
-1 -1 -1 2 2
-1 3 -1 -1 -1
4 -1 4 -1 -1
-1 -1 -1 5 -1
최종값
0 1 -3 2 -4
3 0 -4 1 -1
7 4 0 5 3
2 -1 -5 0 -2
8 5 1 6 0
-1 3 4 5 1
4 -1 4 2 1
4 3 -1 2 1
4 3 4 -1 1
4 3 4 5 -1
경로 찾기
1부터 2까지의 경로 : 1 5 4 3 2
1부터 3까지의 경로 : 1 5 4 3
1부터 4까지의 경로 : 1 5 4
1부터 5까지의 경로 : 1 5
2부터 1까지의 경로 : 2 4 1
2부터 3까지의 경로 : 2 4 3
2부터 4까지의 경로 : 2 4
2부터 5까지의 경로 : 2 4 1 5
3부터 1까지의 경로 : 3 2 4 1
3부터 2까지의 경로 : 3 2
3부터 4까지의 경로 : 3 2 4
3부터 5까지의 경로 : 3 2 4 1 5
4부터 1까지의 경로 : 4 1
4부터 2까지의 경로 : 4 3 2
4부터 3까지의 경로 : 4 3
4부터 5까지의 경로 : 4 1 5
5부터 1까지의 경로 : 5 4 1
5부터 2까지의 경로 : 5 4 3 2
5부터 3까지의 경로 : 5 4 3
5부터 4까지의 경로 : 5 4
'알고리즘 > 이론' 카테고리의 다른 글
| [Algorithm] 연속 구간의 최대 합 구하기 (2) | 2020.05.05 |
|---|---|
| [Algorithm] 불안정정렬 sort, 안정정렬 stable_sort (0) | 2020.03.25 |
| [Algorithm] 벨만포드(Bellman-Ford) 알고리즘 (0) | 2019.11.07 |
| [Algorithm] Prim 알고리즘 (1) | 2019.11.05 |
| [Algorithm] Kruskal 알고리즘 (0) | 2019.11.05 |




