[Algorithm] Two Pointers, 투 포인터
이번 포스팅에서는 Two Pointers에 대해서 알아보도록 하겠습니다.
Two Pointers 는 1차원 배열에서 두 개의 포인터를 조작하여 원하는 결과를 얻는 알고리즘입니다.
여기서 두 개의 포인터를 사용하여 기존의 방식보다 시간을 개선할 수 있습니다.
Two Pointers 의 동작원리, 시간복잡도, C++로 구현한 코드를 보며 이해해보겠습니다.
동작 원리
적절한 예시를 위해 백준에서 Two Pointers 를 사용하는 문제의 에시를 사용하겠습니다.
https://www.acmicpc.net/problem/2003
2003번: 수들의 합 2
첫째 줄에 N(1 ≤ N ≤ 10,000), M(1 ≤ M ≤ 300,000,000)이 주어진다. 다음 줄에는 A[1], A[2], …, A[N]이 공백으로 분리되어 주어진다. 각각의 A[x]는 30,000을 넘지 않는 자연수이다.
www.acmicpc.net
위는 문제 링크고 예제 입력 2를 봅시다.
10 5
1 2 3 4 2 5 3 1 1 2
10개의 자연수의 부분합이 5개 되는 경우의 수를 구해야 합니다.
3중 for문을 사용하여 시작지점, 끝지점, 두 지점의 합을 구해볼 수 있으며 이를 개선하여 부분합 배열을 만든 후 2중 for문으로 구해볼 수 있습니다.
하지만 해당 문제는 두 가지 방법 모두 시간초과가 났고 새로운 방법이 필요했습니다.
그러기 위해 start, end라는 두 개의 포인터를 사용합니다.
start는 부분배열의 앞 쪽을 가르키는 인덱스, end는 부분배열의 뒤 쪽을 가르키는 인덱스입니다.
맨 처음에 두 포인터는 0에서 시작하며 항상 start<=end를 만족해야합니다.
그리고 매 순간마다 부분합 배열의 합과 구해야하는 값을 비교하여 포인터를 이동하게 됩니다.
-
부분합 배열의 합 < 구해야하는 값
end를 오른쪽으로 한 칸 이동하여 부분합 배열의 크기를 증가시킵니다.
-
부분합 배열의 합 >= 구해야하는 값
start를 오른쪽으로 한 칸 이동하여 부분합 배열의 크기를 감소시킵니다.
다음과 같은 동작 과정을 그림을 통해 확인해봅시다.
우선 초기상태입니다.
위에서 말한대로 두 포인터는 0을 가르키고 부분배열의 합도 0입니다.
부분배열의 합이 원하는 값보다 작으므로 end를 증가시킵니다.
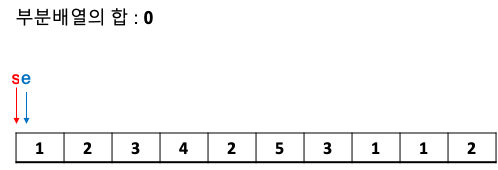
하지만 아직 부분배열의 합은 1로 부족합니다.
마찬가지로 end를 증가시킵니다.

한 번 더 end를 증가시킵니다.

이번에는 부분배열의 합이 5를 초과하였습니다.
start를 증가시킵니다.

이제 부분배열의 합이 원하는 값 5가 되었습니다.
전체 카운트를 하나 증가시킨 후 start를 증가시킵니다.
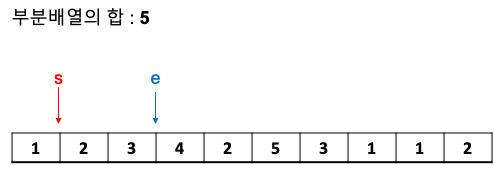
그 이후의 과정은 반복되므로 생략하도록 하겠습니다.
다음과 같이 두 개의 포인터를 조작하여 부분합을 구할 수 있는 이유는 배열의 값들이 자연수 이기 때문입니다.
자연수이기 때문에 end를 증가시키면 부분합이 증가하고 start를 증가시키면 부분합이 감소하는 것을 보장할 수 있지만 음수가 섞여있다는 이를 보장할 수 없으므로 Two Pointers를 사용할 수 없습니다.
시간 복잡도
다음 알고리즘은 두 개의 포인터가 일차원 배열 위를 움직입니다.
그리고 end 포인터가 배열의 마지막에 도달할 경우, 더 이상 구할 수 있는 값이 없으므로 종료합니다.
최악의 경우에도 start와 end가 둘 다 배열의 마지막으로 오는 경우로 O(2n) 입니다.
따라서 Two Pointers 알고리즘의 시간복잡도는 O(n)이 됩니다.
C++로 구현한 코드
위에서 제시했던 백준의 문제를 해결하는 코드입니다.
#include <iostream>
using namespace std;
int board[10001];
int main()
{
int N, M;
cin >> N >> M;
for (int i = 0; i < N; i++)
cin >> board[i];
int answer = 0;
int start = 0;
int end = 0;
int partial_sum = 0;
while (end <= N)
{
if (partial_sum >= M)
partial_sum -= board[start++];
else if (partial_sum < M)
partial_sum += board[end++];
if (partial_sum == M)
answer++;
}
cout << answer << "\n";
}