알고리즘/이론

[Algorithm] 위상정렬

ssung.k 2020. 8. 27. 00:17

위상정렬이란?

위상 정렬은 순서가 정해져있는 작업 차례로 수행해야 할 때, 그 순서를 결정해주는 알고리즘입니다.

그림을 보며 이해해봅시다.

 

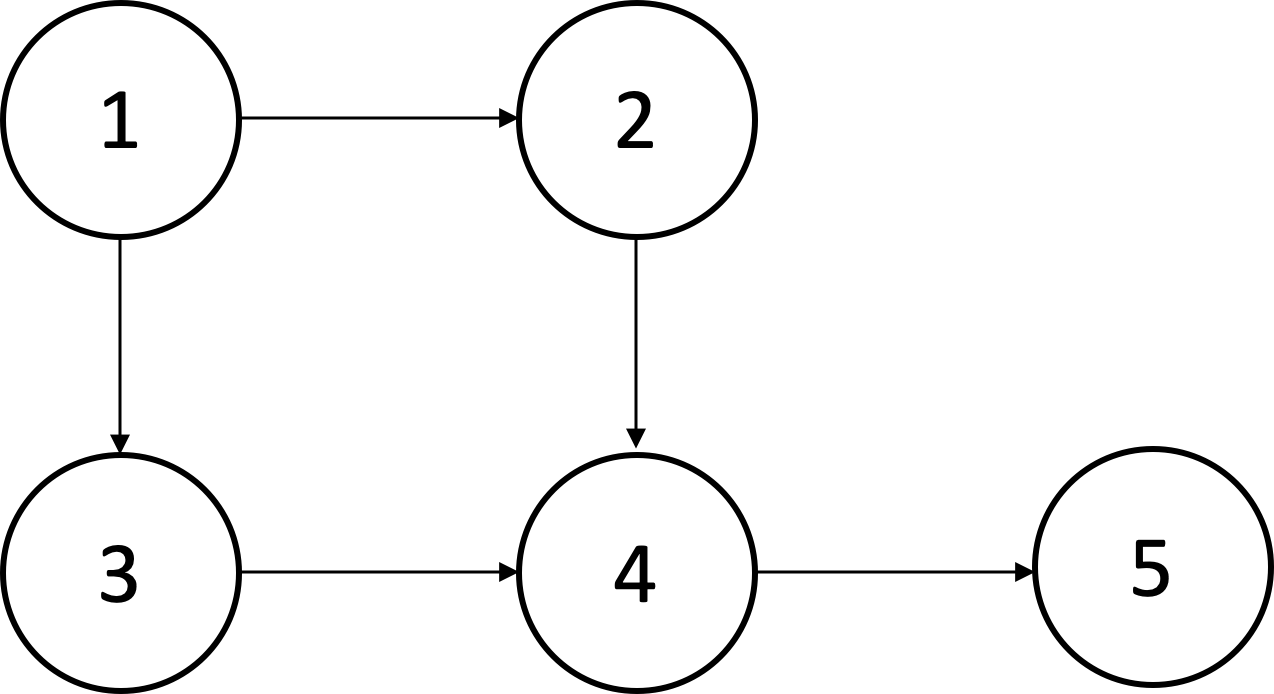
다음과 같은 그래프에서 앞선 작업 2,3이 끝나야 뒤 작업 4가 이루어질 수 있으며 이 때 둘 중 무엇을 먼저 끝내던 규칙에 위배 되지 않기 때문에 경로는 여러 개가 나올 수 있습니다.

단 위상정렬이 성립하기 위해서는 DAG여야 합니다.

DAG란?

Directed Acyclic Graph의 줄임말로 사이클이 존재하지 않는 방향 그래프입니다.

만일 위 그림에서 5이 1에 연결되었다면 시작점이 존재하지 않기 때문에 위상정렬이 성립할 수 없습니다.

 

 

위상 정렬 원리

위상 정렬이 어떤 원리로 동작하는지 살펴봅시다.

위상 정렬을 스택이나 큐를 사용하여 구현할 수 있지만 큐를 사용하는 방법이 더 일반적이니 큐를 사용하는 방법을 알아봅시다.

알고리즘은 다음과 같습니다.

  1. 각 노드들의 진입 차수 계산
  2. 진입 차수가 0인 노드들을 큐에 삽입
  3. 큐에서 노드를 꺼내 연결된 간선을 제거
  4. 제거로 인해 진입 차수가 0이 된 노드를 큐에 삽입
  5. (3)~(4) 번을 반복하며 큐가 비었으면 종료

 

위 예시에 대해 각각의 알고리즘을 적용해봅시다.

 

우선 각 노드의 진입 차수를 계산해줍니다.

노드 1 2 3 4 5
차수 0 1 1 2 1

 

차수가 0인 노드 1을 큐에 삽입합니다.

// queue
1

 

큐에서 노드 1을 꺼내 연결된 간선을 제거합니다.

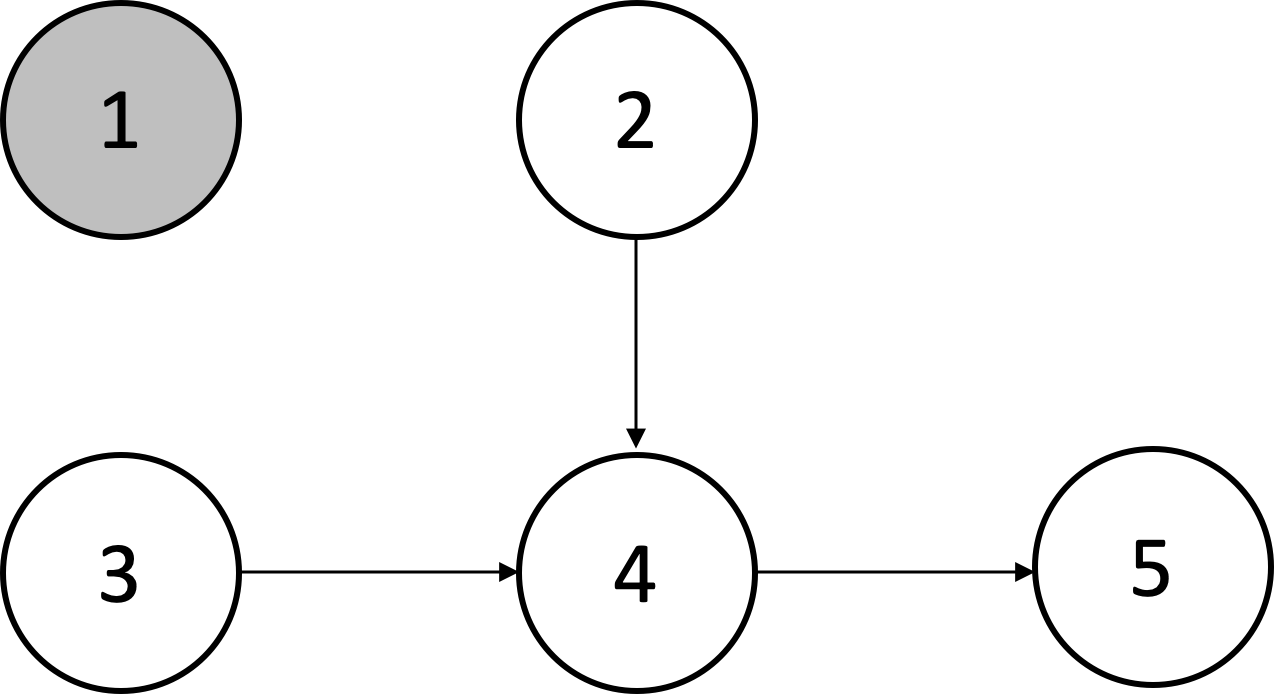
노드 1 2 3 4 5
차수 0 0 0 2 1

 

 

 

간선 제거 이후 차수가 0이 된 노드 2,3 을 큐에 삽입합니다.

//queue
2 3

 

노드 2를 꺼내 간선을 제거하고, 다시 노드 3을 꺼내 간선을 제거합니다.

(같은 동작을 반복하여 한 번에 나타내었습니다.)

노드 1 2 3 4 5
차수 0 0 0 0 1

 

차수가 0인 노드 4를 큐에 삽입합니다.

// queue
4

 

큐에서 노드 4를 꺼내고 간선을 제거합니다.

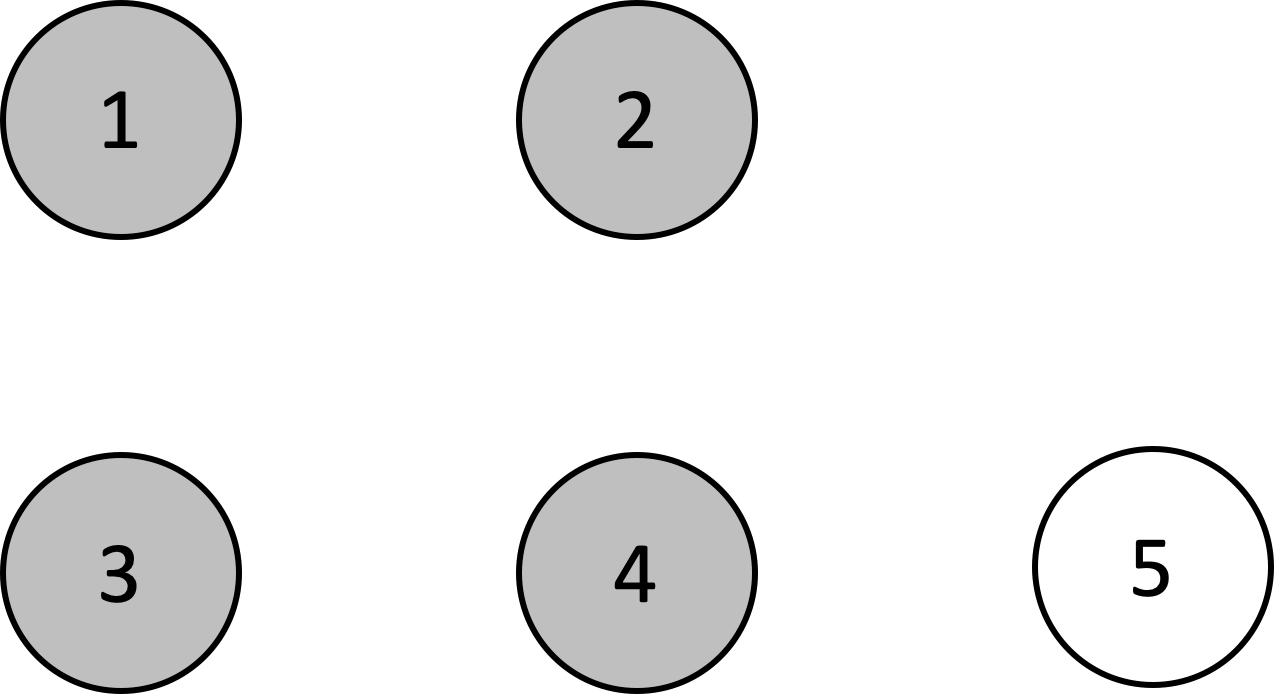
노드 1 2 3 4 5
차수 0 0 0 0 0

 

 

노드 5를 큐에 넣습니다.

// queue
5

 

노드 5를 큐에서 꺼내 관련 간선을 제거합니다. 물론 관련 간선은 존재하지 않습니다.

마지막으로 큐가 비었으므로 반복을 종료합니다.

 

C++ 코드

위의 위상정렬 알고리즘을 C++로 구현하였습니다.

#include <iostream>
#include <vector>
#include <queue>

#define MAX 10

using namespace std;

int input_degree[MAX];
vector<int> adjust[MAX];
int result[MAX];

int main()
{
    queue<int> q;
    int N, K;
    cin >> N >> K;

    for (int i = 0; i < K; i++)
    {
        int n1, n2;
        cin >> n1 >> n2;
        adjust[n1].push_back(n2);
        input_degree[n2]++;
    }

    for (int i = 1; i <= N; i++)
        if (!input_degree[i])
            q.push(i);

    for (int i = 1; i <= N; i++)
    {
        if (q.empty())
        {
            cout << "cycle\n";
            return 0;
        }

        int now = q.front();
        q.pop();

        result[i] = now;

        for (int i = 0; i < adjust[now].size(); i++)
        {
            int next = adjust[now][i];
            input_degree[next]--;
            if (input_degree[next] == 0)
                q.push(next);
        }
    }

    for (int i = 1; i <= N; i++)
        cout << result[i] << " ";

    cout << "\n";
}

 

input은 첫번째 줄에 노드의 개수 N, 간선의 개수 K가 들어오고 이어서 K만큼 간선 순서 X Y가 주어집니다.

[ input ]
4 4
1 2 
1 3
2 4
3 4
  
[ output ]
1 2 3 4

 

저작자표시