| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 |
- AWS
- Baekjoon
- 파이썬
- 장고
- 파이썬 알고리즘
- 알고리즘 풀이
- Algorithm
- Django
- django widget
- js
- 알고리즘 연습
- javascript
- 백준
- django ORM
- API
- java
- web
- HTML
- DRF
- CSS
- Git
- form
- PYTHON
- es6
- django rest framework
- 알고리즘 문제
- react
- 알고리즘
- MAC
- c++
- Today
- Total
수학과의 좌충우돌 프로그래밍
[인공지능] PCA (1) Principle Component Analysis 란? 본문
실무에서 접하게 되는 데이터는 feature의 수가 대체로 큽니다. 이는 생각보다 더 큰 문제로 작용합니다. 당연히 데이터의 크기가 크다보니 학습 속도에도 영향을 미치고 다루기가 쉽지 않습니다. 따라서 차원의 수를 축소하는 방법이 여러가지가 있는데 그 중에서 대표적인 차원 축소 알고리즘, PCA 에 대해서 알아보도록 하겠습니다.
PCA 의 원리
PCA 가 어떤 과정을 통해서 차원을 축소하는지 알아보도록 하겠습니다. 우선 다음과 같은 2차원 데이터가 있을 때, 현재 목표는 2차원 데이터를 1차원으로 축소하는 것입니다.

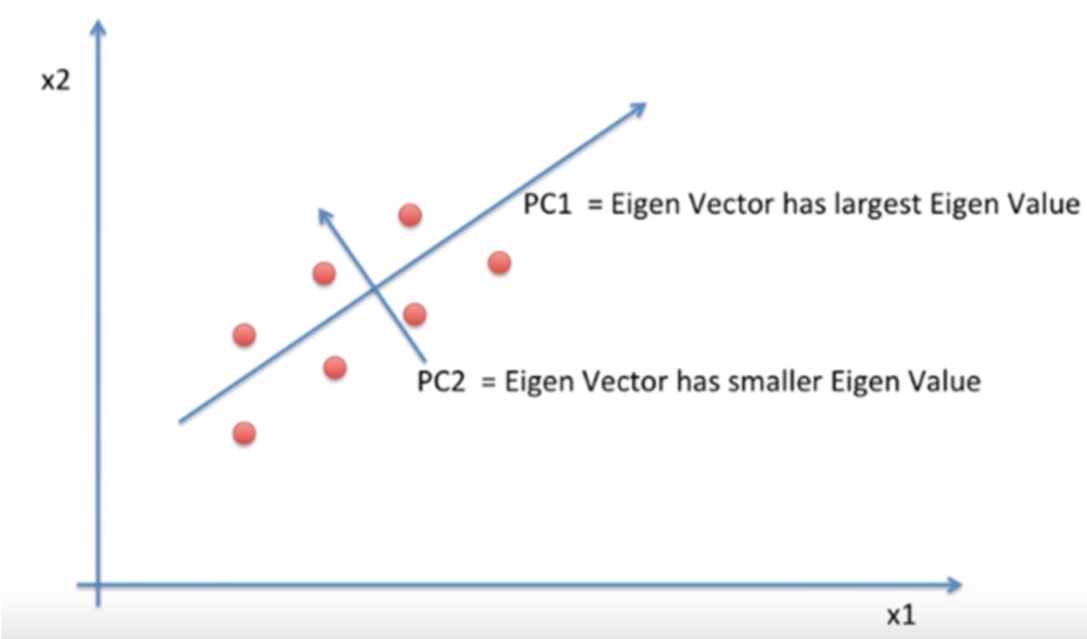
PCA 는 데이터를 1차원으로 축소하는 방법으로 정사영을 사용합니다. 정사영을 하기 위해서는 축을 선택해야 하는데 축이 될 선택지는 다양합니다. 아래 그림과 같이 x1 축으로 축소를 할 수 도 x2 축으로 축소를 할 수 도 있습니다. 하지만 그림을 보면 알 수 있듯이 이들은 문제가 있습니다.
기존 2차원일 때는 거리를 두고 있던 점들이 차원이 축소되며, 정사영 되면서 겹치게 되는 문제가 발생합니다. 이 과정을 통해 기존의 정보가 유실되고 맙니다.


따라서 다음과 같이 x1, x2 축이 아닌 새로운 축을 찾아야 합니다. 아 물론 x1, x2 축이 유실이 가장 적게 일어나는 축이 될 수도 있겠죠. 축은 각 점들이 퍼져있는 정도인 분산이 가장 크게 되도록 잡아야 할 것입니다. 그리고 이렇게 찾은 축을 principal component 줄여서 PC 라고 합니다.

PC 를 찾기 위해서는 covaiance matrix 의 eigen vector 값을 찾아야 하고 이 값 중 가장 큰 값이 우리가 원하는 PC 에 만족합니다.
covariance matrix
위의 과정을 이해하기 위해서 하나씩 step 을 밟아보도록 하겠습니다. 먼저 covariance matrix 가 무엇인지 알아보도록 하죠.
covariance
다시 covariance 부터 알아보면 공분산이라고도 하며, 둘 이상의 변량이 연관성을 가지며 분포하는 모양을 전체적으로 나타낸 분산을 말합니다.
공분산은 다음과 같이 구할 수 있습니다.

또 분포하는 모양에 따라서 다음과 같이 관계를 나눌 수 있습니다.

두 확률 변수 X,Y 에 대해
(a) X가 증가할 때 Y도 증가하면 공분산이 0보다 큰 값을 가지며 양의 상관관계에 있다고 합니다.
(b) X가 증가할 때 Y는 감소하면 공분산이 0보다 작은 값을 가지며 음의 상관관계에 있다고 합니다.
(c) X와 Y과 연관이 없으면 공분산이 0 값을 가지며 관계가 없다고 합니다.
covariance 의 문제점
이번 주제와는 큰 연관 없지만 convariance 는 한 가지 문제점이 있습니다. 측정 단위에 값이 영향을 미치는데 이를 not scale free 라고 합니다. 그렇기 때문에 부호를 통해 어느 관계를 가지고 있는지는 알 수 있지만 그 관계의 크기를 나타내는데는 한계가 있습니다.

다음과 같은 두 데이터 모두 강한 선형 관계에 있지만 A 데이터가 B 데이터가 보다 기대값이 훨씬 크므로 공분산도 A 데이터가 훨씬 크게 됩니다.
이러한 문제점을 해결하기 위해서 correlation , 상관계수 라는 개념이 도입되었습니다. 상관계수는 공분산의 단점을 보완하고자 분산 등의 특정 값으로 나눠주는 단위화 작업을 거침으로서 단위의 절대적인 크기에 영향을 받지 않게 합니다. 이에 대해선 별도의 포스팅에서 더 자세히 알아보도록 하겠습니다.
covariance matrix
이제 covariance matrix , 공분산 행렬에 대해서 알아보도록 하겠습니다.
n 명의 사람에 대해, d 개의 feature 가 있다면 이 데이터를 다음과 같이 행렬 X 로 표현할 수 있습니다. 주의할 점은 데이터를 있는 그래도 가져오지 않고 각 열마다 feature 에 대한 평균 값으로 빼므로서 표현하고 각 열에 대해 평균은 0이 됩니다.

데이터 X 에 대해, 다음과 같은 연산을 하게 됩니다. 여기서 dot 은 내적 연산을 의미합니다.
행렬의 i행 j열의 의미는 i번째 특징과 j 번째 특징이 얼마나 유사한가를 나타내줍니다.

만약 n 값이 증가하면 행렬의 성분 값이 계속 커지기 때문에 n 을 나누어 줌으로서 해결할 수 있습니다.

내적과 상관계수
내적과 두 특징을 나타내는 상관계수 가 무슨 연관이 있을까요?
내적
내적의 의미를 생각보도록 합시다. 내적의 기하학적 의미를 생각해보면 한 벡터를 다른 벡터 위로 정사영 시킨 길이 를 의미합니다.

다음과 같은 그림에 대해서 "a 의 변화를 b 가 얼마나 잘 나타낼 수 있는가" 라고 생각할 수 있고 이는 수식으로 a*b / |b| 다음과 같습니다.
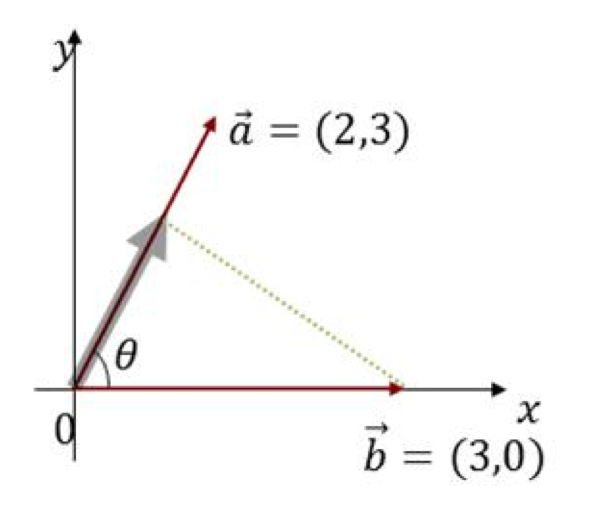
같은 맥락으로 "b의 변화를 a가 얼마나 잘 나타낼 수 있는가" 라고 생각할 수 있으며 수식으로 a*b / |a| 다음과 같습니다.
더 나아가서 "a,b 가 서로의 변화를 얼마나 잘 표현할 수 있는가"에 대해서는 수식으로 a*b / |a|*|b| 다음과 같이 나타냅니다.
상관계수
상관계수 r 에 대해 다음과 같은 식이 성립합니다.


다음과 같이 치환하면,
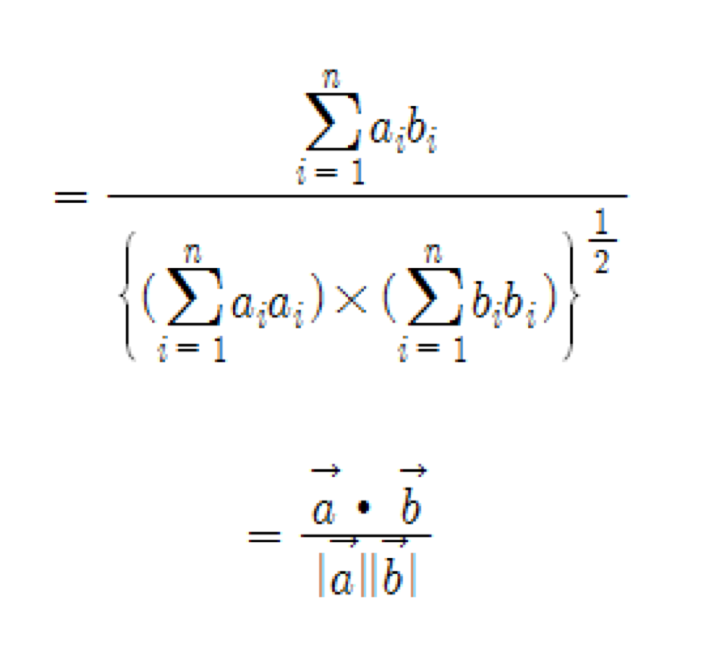
내적과 같은 식을 얻을 수 있습니다. 내적에서 봤듯이 이는

를 나타내게 됩니다.
'인공지능' 카테고리의 다른 글
| [인공지능] PCA (2) python 을 사용한 PCA 실습 (0) | 2019.08.20 |
|---|

